PBRT 第十章笔记 | Notes for PBRT Chapter 10 - Textures

programming | reading notes , , Comments

10.1 Sampling and Antialiasing

从第七章引入了走样的概念以来，这种现象就是在现有的基于采样的方式中不可解决的。我们能做的只能使用一系列方法降低走样对视觉的影响。

值得庆幸的是，在材质这一方面上，我们可以在采样之前就提前去除材质中的高频信息，或是在采样过程中使用特殊方法避免引入高频信息，从而减小采样时的走样现象。对于应用于材质上的反走样方法，主要的研究问题有以下两点：

  1. 确认材质的采样率：给定场景的采样率，我们需要确定在某一物体上的材质对应的采样率
  2. 确定采样方法：在确定了材质的采样率后，需要寻求指导采样进行的算法以去除高于采样率的信息。

10.1.1 材质采样率的确定

考虑一个定义在某个表面上的一个材质函数 T(x)T(x) ，当我们忽略由于可见性导致的突变以外，这个材质函数其实也可以视作定义在图像平面上的另一个函数 T(f(x,y))T(f(x,y)) 。这种从像素位置和材质位置的映射，结合二者采样率的差异，是求解材质在屏幕空间上对应的最高采样率的核心。

对于大多数的场景几何情况、投影方法和材质映射，我们通常很难找到这一映射的解析解。但对于反走样算法而言，我们只需要找到像素采样位置的变化对材质采样位置的影响即可。我们通常使用一阶偏导数近似这一结果：

f(x′,y′)≈f(x,y)+(x′−x)∂f∂x+(y′−y)∂f∂yf(x',y') \approx f(x,y) + (x'-x){\partial f \over \partial x} + (y'-y){\partial f \over \partial y}

这里使用的偏导数可以从 RayDifferential 中得到。我们会使用从图像坐标到世界坐标的函数 p(x,y)p(x,y) 的偏导数和从图像坐标到材质 uv 的函数 u(x,y),v(x,y)u(x,y), v(x,y) 的偏导数解决这一问题。在生成 SurfaceInteraction 时计算偏导数的具体方法如下：

首先，我们假定微分光线与表面的交点均在一个由法线和光线交点确定的平面上，利用微分光线与平面的交点位置和光线交点位置的差异可以估算一阶偏导数：

∂p∂x≈px−p, ∂p∂y≈py−p{\partial p \over \partial x} \approx p_x - p,\ {\partial p \over \partial y} \approx p_y - p

其次，利用该平面上 uv 的分布情况（可以直接在材质中得到），我们可以假定对于微分情况下，有近似：

p′=p+Δu∂p∂u+Δv∂p∂v(px′−pxpy′−pypz′−pz)=(∂px/∂u∂px/∂v∂py/∂u∂py/∂v∂pz/∂u∂pz/∂v)×(ΔuΔv)p' = p + \Delta_u{\partial p \over \partial u} + \Delta_v{\partial p \over \partial v}\\ \left(\begin{matrix} p'_x-p_x\\ p'_y-p_y\\ p'_z-p_z \end{matrix}\right) = \left(\begin{matrix} {\partial p_x / \partial u} & {\partial p_x / \partial v}\\ {\partial p_y / \partial u} & {\partial p_y / \partial v}\\ {\partial p_z / \partial u} & {\partial p_z / \partial v} \end{matrix}\right) \times \left(\begin{matrix} \Delta_u\\ \Delta_v \end{matrix}\right)

此时令 p′=px,p′=pyp' = p_x, p' = p_y 带入就可以得到对应的 ∂u/∂x,∂u/∂y,∂v/∂x,∂v/∂y{\partial u/\partial x},{\partial u/\partial y},{\partial v/\partial x},{\partial v/\partial y} 这里每组是两个浮点数，而输入的 ∂p/∂x,∂p/∂y{\partial p/\partial x},{\partial p/\partial y} 则分别有三个自由度，因此这是一个使用三个方程求解两个未知量的方程，这说明这其中至少有一个方程是多余的。为了选定用于求解的方程组，一种求解方法是做 ∂p/∂u,∂p/∂v{\partial p/\partial u},{\partial p/\partial v} 的叉乘，选择叉乘值中较小的两个维度输入线性方程组，而在 SurfaceInteraction 中，这个叉乘的值恰好就是法线 nn 。

即便如此，在 ∂p/∂u,∂p/∂v{\partial p/\partial u},{\partial p/\partial v} 共线时，也是无法求解线性方程的，此时 PBRT 会将对应的导数值设为零。

10.1.2 对材质进行滤波

为了去除超过了采样的纳什限制的频率，需要先对原始的材质进行 sincsinc 滤波：

Tb′(x,y)=∫−∞∞∫−∞∞sinc⁡(x′)sinc⁡(y′)T′(f(x−x′,y−y′))dx′dy′T_{b}^{\prime}(x, y)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \operatorname{sinc}\left(x^{\prime}\right) \operatorname{sinc}\left(y^{\prime}\right) T^{\prime}\left(f\left(x-x^{\prime}, y-y^{\prime}\right)\right) \mathrm{d} x^{\prime} \mathrm{d} y^{\prime}

接着对这个滤波后的函数在像素的范围内对一个权重函数（pixel filter）做卷积：

Tf′(x,y)=∫−yWidthyWidth∫−xWidthxWidthg(x′,y′)Tb′(x−x′,y−y′)dx′dy′T_{f}^{\prime}(x, y)=\int_{-yWidth}^{yWidth} \int_{-xWidth}^{xWidth} g\left(x^{\prime},y^{\prime}\right) T_{b}^{\prime}\left(x-x^{\prime}, y-y^{\prime}\right) \mathrm{d} x^{\prime} \mathrm{d} y^{\prime}

在实际使用中，常常对这一过程进行一系列的简化，如在两步中均使用最简单的 box filter 计算算术均值。因为在采样后所有样本还需要经过图像重建的过程，就算使用一种简单的滤波方式得到的次优解也能提供优秀的视觉效果。

如果我们能够提前得知组成材质的各个频率组成部分，就可以通过 clamping 的方法，通过将更高频的部分替换为其均值以完成滤波。这一方法被广泛应用于程序生成的材质的反走样中。

最终还有一种最通用的方式完成对材质的反走样处理：超采样。这和图像空间上的超采样是大同小异的。这种方法仍被使用的原因在于，即使它相比于其它材质上的滤波方法而言消耗巨大，但与在图像空间上面进行超采样而言它的效率仍然是较高的。

10.1.3 镜面反射和折射情况下的光线微分 ⚠️

由于光线微分在对材质滤波的过程中十分有效，我们很自然地会希望将它拓展到镜面反射和折射后的光线上。

这一过程首先开始于使用 ∂p/∂x, ∂p/∂y\partial p / \partial x,\ \partial p / \partial y 估计微分光线的交点（也是出射微分光线的起始点），与计算这一值时采用的同平面假设不同，在计算镜面反射和折射的微分光线时考虑了法线在这一方向上的变化。

考虑镜面反射的光线方向方程：

ωi+ωo=2(ωo⋅n)n\omega_i + \omega_o = 2(\omega_o \cdot \mathbf{n})\mathbf{n}

对 ωi\omega_i 求偏导可以得到：

∂ωi∂x=∂∂x(−ωo+2(ωo⋅n)n)=−∂ωo∂x+2((ωo⋅n)∂n∂x+∂(ωo⋅n)∂xn)\begin{aligned}\frac{\partial \omega_{\mathrm{i}}}{\partial x} &=\frac{\partial}{\partial x}\left(-\omega_{\mathrm{o}}+2\left(\omega_{\mathrm{o}} \cdot \mathbf{n}\right) \mathbf{n}\right) \\&=-\frac{\partial \omega_{\mathrm{o}}}{\partial x}+2\left(\left(\omega_{\mathrm{o}} \cdot \mathbf{n}\right) \frac{\partial \mathbf{n}}{\partial x}+\frac{\partial\left(\omega_{\mathrm{o}} \cdot \mathbf{n}\right)}{\partial x} \mathbf{n}\right)\end{aligned}

其中点乘的微分可以进一步分解如下：

∂(ω0⋅n)∂x=∂ω0∂x⋅n+ω0⋅∂n∂x\frac{\partial\left(\omega_{0} \cdot \mathbf{n}\right)}{\partial x}=\frac{\partial \omega_{0}}{\partial x} \cdot \mathbf{n}+\omega_{0} \cdot \frac{\partial \mathbf{n}}{\partial x}

考虑到对于一个微分光线的入射方向 ω\omega （即从视点出发被反射的出射方向），就能很容易的得到新光线的微分情况：

ω≈wi+∂ωi∂x=ωi−∂ωo∂x+2((ωo⋅n)∂n∂x+(∂ω0∂x⋅n+ω0⋅∂n∂x)n)\begin{aligned} \omega & \approx w_i + {\partial\omega_i \over \partial x}\\ & = \omega_i - \frac{\partial \omega_{\mathrm{o}}}{\partial x} + 2\left(\left(\omega_{\mathrm{o}} \cdot \mathbf{n}\right) \frac{\partial \mathbf{n}}{\partial x}+\left(\frac{\partial \omega_{0}}{\partial x} \cdot \mathbf{n}+\omega_{0} \cdot \frac{\partial \mathbf{n}}{\partial x}\right) \mathbf{n}\right) \end{aligned}

对于镜面折射的情况只需要改变对应的光线方程即可得到类似的新微分光线。

10.2 Texture Coordinate Generation

Texture 类型储存了一个指向了二维或三位的映射函数以在各个点上计算材质坐标。在 PBRT 中，材质坐标被使用 s,ts,t 表示，以区分于属于表面属性的 uv 坐标。

最常用的 2D 材质映射基类 TextureMapping2D 中只含有一个接口函数 Point2f Map(const SurfaceInteraction &si, Vector2f *dstdx, Vector2f *dstdy) 。它接收着色点的信息，并返回对应的材质坐标与偏导数信息。

10.2.1 二维 (u,v)(u,v) 映射

最简单的映射方法即直接使用 SurfaceInteraction 中的 uv 信息作为材质的 st 坐标。UVMapping2D 类实现了一个简单的缩放和偏移映射，它在构建时传入各个方向上的缩放比例 su, sv 和偏移值 du, dv ，并以此计算偏导数和 st 坐标

10.2.2 球形映射

这种映射方法首先将物体从世界坐标变换到材质坐标系中，再投影到一个以原点为圆心的球面上以计算 st 值，球面的函数则简单地使用极坐标系下的 θ,ϕ\theta, \phi 值完成存储。

然而这种映射方式的坐标系是不连续的，特别是在 t=1t = 1 的位置上，这里的 tt 值会在这条边界线上发生跳变，因此需要特别处理这种特殊情况。

10.2.3 圆柱映射

与球形映射不同的是这种方法会将物体投影到圆柱的侧面上，它也存在和球型映射相似的微分不连续问题。

10.2.4 平面映射

这种方法直接地使用一组向量作为基，将物体上的点投影在这一平面坐标系上，最后加上偏移值作为 st 坐标。

10.2.5 三维映射

除了 2D 的材质外，可能还会见到一些 3D 的体积材质，它使用了一个 WorldToTexture 变换将世界坐标转换为 3D 的材质内坐标。

10.3 Texture Interface and Basic Textures

材质接口是一个模板抽象类，它使用 T Evaluate(const SurfaceInteraction &) 函数从给定的表面位置返回材质内容。

10.3.1 常数材质

这种材质无论在什么位置都返回一个预定义的常数

10.3.2 乘积材质

这个材质中包含了两类子材质，它们 Evaluate 的结果会被相乘，并返回与第二个材质类型匹配的值，相当于使用第一种材质作为第二种材质的缩放因数。

10.3.3 混合材质

这种材质使用一个浮点数材质（如噪声材质）混合两个同类的材质。

10.3.4 双线性插值材质

这是一类特殊的材质，它返回在四个角点上进行双线性插值的结果。

10.4 Image Texture

ImageTexture 类保存了一个离散的二维图像，它使用这个图像在 st 坐标下重建可以在任意位置被采样的连续图像方程。

和其它材质类型不同的是，ImageTexture 类型需要两个模板参数，分别代表储存时的类型和输出的类型。例如它可以输入以 RGBSpectrum 储存的图像，并输出以 SampledSpectrum 储存的值。

在创建一个 ImageTexture 对象时，需要传入的信息包括了图像的文件名、颜色矫正和采样参数等。构造函数会使用这些参数初始化一个 MIPMap 对象以储存图像数据。这个对象也同时负责了重建图像和抗锯齿的功能。

10.4.1 ImageTexture 的内存管理

由于同一个材质可能会被多个物体引用多次，因此在储存时对于不同的材质只会分别储存一份，并通过静态接口 ImageTexture::GetTexture() 使用给定的材质描述块索引对应的 MIPMap 对象。

图像的读入通过 ReadImage() 接口完成，读入的 texel 会被 convertIn() 接口转换为储存类型，并完成 gamma 矫正等调整过程。

10.4.2 ImageTexture 的使用

此处基本上就是调用了数个接口：

1
2
3
4
5
6
7
8
Treturn Evaluate(const SurfaceInteraction &si) const {
		Vector2f dstdx, dstdy;
		Point2f st = mapping->Map(si, &dstdx, &dstdy);
		Tmemory mem = mipmap->Lookup(st, dstdx, dstdy);
		Treturn ret;
		convertOut(mem, &ret);
		return ret;
}

10.4.3 MIP Maps

图像上的材质已经被以固定的采样率采样完成了，当查找时的屏幕对应的频率小于图像频率时就会出现走样的问题。下图展示了一种可能的采样需求，它由采样点 (s,t)(s,t) 和两个对于屏幕坐标的偏导数 dstdx, dstdy 组成：

和在图像上的反走样不同，材质上的反走样具有以下特点：

  1. 采样材质的开销远小于采样图像的开销
  2. 图像材质的最高频率是已知的
  3. 材质的采样率在图像的各个位置上变化很大，要求要对材质在不同位置以不同的采样率采样

PBRT 的 MIPMap 类型中实现了两种对材质的采样方式，分别是较快的三线性插值和质量较高的 Elliptically Weighted Averaging (EWA) 滤波法。这两种采样方式均使用了一种金字塔结构的图像层级加速结构，从全分辨率的底层开始，每一层的长宽都是上一层的一半。

为了便于生成图像的层级，如果用户输入的图像分辨率不是 2 的整数幂次方，PBRT 会使用两轮重采样方法，分别将它的长宽更改为比原始长宽大的第一个幂次方值（如 15×515\times 5 的输入会被转换为 16×816 \times 8 作为底层的分辨率），这是第七章中的一系列重采样方法的应用之一。对于金字塔结构的剩余层级的初始化则，则直接使用上一层对应的四个 texel 计算均值。

特别需要注意的是，PBRT 中处理连续域坐标和离散域坐标的方法是将离散坐标置于每个单位连续域区间的中心，即通过在离散值上加上 0.5 可以得到在连续区域上的位置，如图所示：

由于对于图像的采样是频繁且具有一定关联性的，这种金字塔结构使用了自定义的 BlockedArray 结构以增加 cache 命中率。

10.4.4 Isotropic Triangle Filter

这种最简单的滤波方法假设滤波的范围是一个正矩形区域（即 dstdx = dstdy ），如果输入的两个偏导数不同，则会使用较大的那个偏导数作为矩形的半边长。这种滤波方法的流程如下：

  1. 对于滤波区域的宽度 ww 找到一个 mipmap 层级 ll ，使得采样范围可以覆盖 4 个采样点：

    1w=2nTotalLevels−1−l{1 \over w} = 2^{nTotalLevels - 1 - l}

  2. 对于上述解得的浮点数 ll 两侧的整数层级，分别使用双线性插值（即三角滤波）获得一个 texel 值

  3. 对于两个层级的 texel 值，用 ll 值再进行一次线性插值，最后返回插值的结果

这种滤波方式的最大问题在于它在滤波的滤波范围各向异性较为明显的位置（如球纹理映射的极点、倾斜视角的边缘附近）得到的结果会显得比较模糊。

10.4.5 Elliptically Weighted Average ⚠️

这种算法使用一个椭圆拟合滤波的范围，椭圆的两个半长轴即为两个方向偏导数。与上述各向同性的滤波方法不同的是，这一方法使用较小的方向导数选择滤波 MIPMap 层级，但它也同样会在两个不同的层级之间做插值以增加精度。

在给定层级执行 EWA 滤波的主要方法是 MIPMap<T>::EWA() ，它的流程如下：

  1. 首先将 st 坐标系转换为对应层级中整数的 texel 坐标系上

  2. 计算椭圆在 texel 坐标系中的隐式方程

    e(s,t)=As2+Bst+Ct2<Fe(s,t) = As^2 + Bst + Ct^2 < F

  3. 找到这个椭圆在 texel 坐标系内的 AABB

  4. 遍历这个包围盒内的所有坐标，对于在椭圆内的 texel 使用高斯函数加权求平均，最后返回加权均值

10.5 Solid and Procedural Texturing

根据之前的定义，材质的坐标是由 (s,t)(s,t) 这个二维的值所描述的，我们不难将其拓展到更高的维度上。

三维的材质也被称为 Solid Texture ，由于物体本身就定义在三维空间中，这种材质也是非常常见的。

三维的材质也带来了材质表示的问题：三维的表所需要的内存空间非常巨大，而且相比可以从图像中得到的二维材质而言更难获取。因此就引入了程序生成的材质的概念：

程序生成的材质相当于基于事先设定好的参数，利用材质坐标系上使用某种映射生成所需的图案。常见的映射包括了使用 uv 坐标、深度、法线等信息作为颜色，以及一些常见的几何形状如棋盘等。程序生成的材质通常有以下特点：

  1. 空间消耗极小，通常只需要储存不多的参数
  2. 可以拥有无穷的细节
  3. 时间消耗较大，也因此给反走样带来了困难

10.5.1 UV 材质

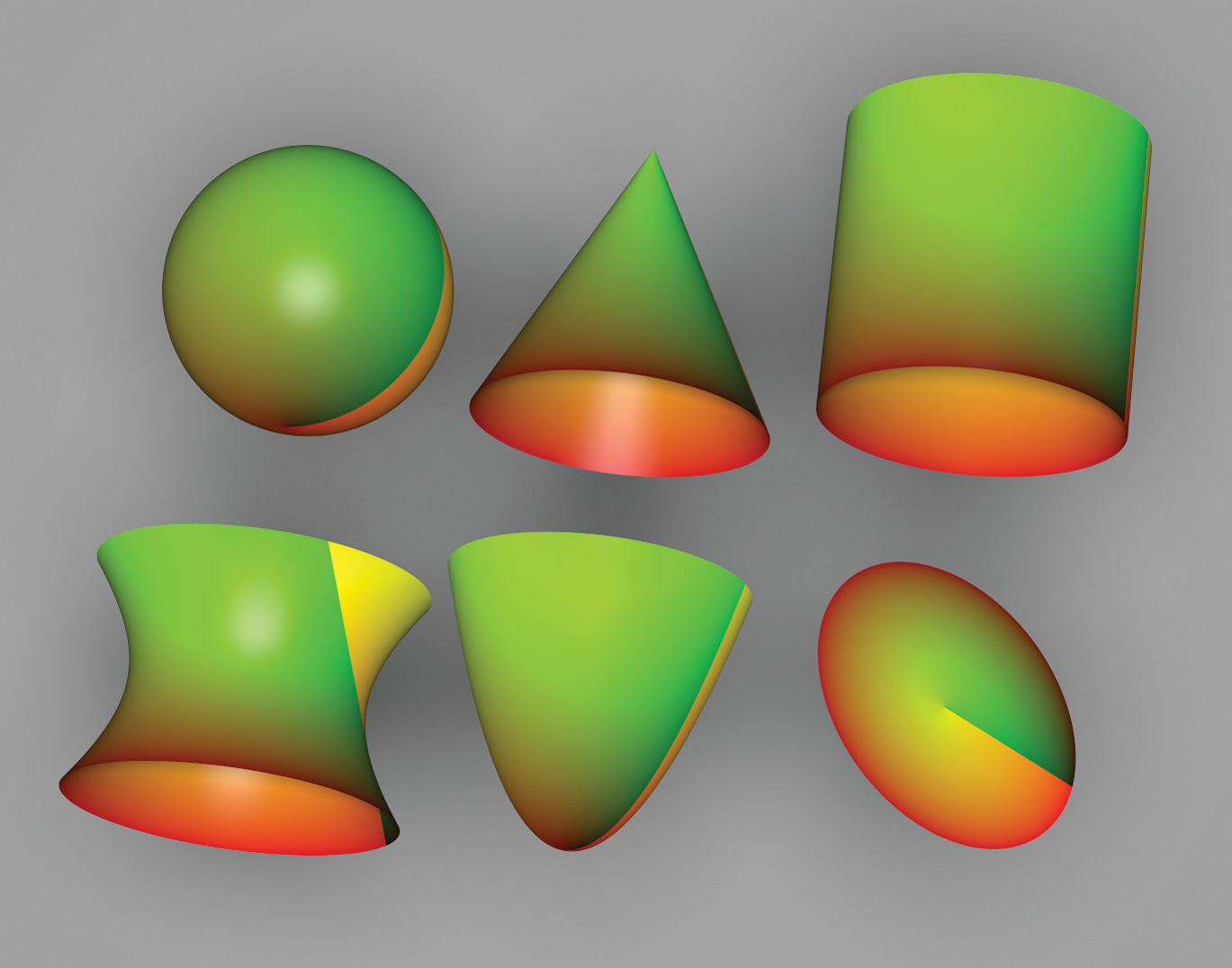
这是一种最简单的程序生成的材质，它可以通过简单地将 st 坐标分别作为 RG 通道的值，并将 B 通道设置为 0 实现。这种材质主要应用于 debugging 。

10.5.2 棋盘材质

这是一种等距间隔分布的棋盘状图形。为了方便实现，在 PBRT 中，这种材质里的每个矩形在 st 坐标下的边长均为 1 。PBRT 还另外提供了两个材质以填充棋盘图形的不同区域。

Chessboard 材质的反走样

在这一反走样策略中，采样区域被认为是采样点周围的一个与屏幕方向偏导有关的 AABB。这虽然增加了模糊程度，但在实现上更加友好，这种算法的实现过程非常简单：

  1. 如果 AABB 在同一材质内，直接采样当前材质即可
  2. 如果 AABB 跨越了不同材质，分别采样两种材质，并使用各个材质占 AABB 的面积比例作为权重加权平均

10.5.3 三维棋盘

这种材质将二维的棋盘材质拓展到了三维空间中

10.6 Noise

为了给材质增加更多的细节，可以引入一些可控、不均匀的微小变化，这就是噪声。噪声材质要求在材质坐标系内拥有连续可、计算且没有明显的重复性的函数。

噪声函数完成了这种从 Rn→[−1,1]R^n \to [-1, 1] 的映射，它们往往拥有明确的频率区间，可以控制材质中的频率组分，因此便于滤波的进行。

一种最简单的噪声是 value noise 。它在三维空间中定义了一系列定位点，每个点储存了一个随机数值。在进行采样时，它会找到采样点周围的数个定位点，并使用任意插值方法（如三线性插值，或更复杂的多项式插值）混合它们的噪声值。

10.6.1 Perlin Noise

Perlin noise 在任何整数点的位置上的值均为 0 ，并使用定义在各个整数点上的一个随机梯度决定噪声值。在 Perlin Nosie 上采样的步骤如下：

  1. 计算采样点周围的整数点坐标

  2. 计算梯度与指向采样点的向量的点乘，依次代表各个梯度对采样点的影响

  3. 将该权重进行平滑处理，这一操作使得结果具有了连续的一、二阶导数，插值前使用的平滑函数如下：

    wa=6(a−ai)5−15(a−ai)4+10(a−ai)3w_a = 6(a-a_i)^5 - 15(a-a_i)^4 + 10(a-a_i)^3

  4. 使用三线性插值混合这 8 个影响值

在实际实现中，PBRT 还为了提高速度加入了大量 trick ，包括使用预设定的随机数表 NoisePerm 多级索引噪声组成等方法。其中计算梯度贡献度的函数如下：

1
2
3
4
5
6
7
inline Float Grad(int x, int y, int z, Float dx, Float dy, Float dz) {
    int h = NoisePerm[NoisePerm[NoisePerm[x] + y] + z];
    h &= 15;
    Float u = h < 8 || h == 12 || h == 13 ? dx : dy;
    Float v = h < 4 || h == 12 || h == 13 ? dy : dz;
    return ((h & 1) ? -u : u) + ((h & 2) ? -v : v);
}

10.6.2 Random Polka Dots

这种材质将表面分为均等的子区域（类似棋盘），每个区域中均会有 50% 的概率出现一个半径为 0.35 的圆形。它的实现方式和棋盘材质其实大同小异，只不过在区分两类材质的覆盖位置时使用了增加了随机性的算法。

10.6.3 Noise Idioms and Spectral Synthesis

对于很多应用场景而言，将多种不同的噪声以某种权重组合起来是非常常见的做法。当我们直到某一噪声函数的频率组成部分时，当我们对输入乘以一个缩放常数之后，新的噪声的频率也能非常容易地得到。

fs(x)=∑iwif(six)f_s(x) = \sum_i w_if(s_ix)

Fractional Brownian Motion (FBM)

通常来说，缩放和权重均是按两倍的比例提升的，每增加一级噪声，其权重一般是上一级的一半，而频率是上一级的两倍。当这种策略应用于 Perlin Noise 上时，著名的分型杂色 fractional Brownian motion (fBm) 就诞生了。下图展示了层次数量为 3 和 6 情况下的一维分型杂色的图像。

由于分型噪声这种由多个频率依次递进的部分组成的性质，在抗锯齿的过程中，我们可以很容易地通过取最长的采样区间半径来确定实际上应该使用多少层噪声。完整的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Float FBm(const Point3f &p, const Vector3f &dpdx, const Vector3f &dpdy,
          Float omega, int maxOctaves) {
    // Compute number of octaves for antialiased FBm
    Float len2 = std::max(dpdx.LengthSquared(), dpdy.LengthSquared());
    Float n = Clamp(-1 - .5f * Log2(len2), 0, maxOctaves);
    int nInt = std::floor(n);

    // Compute sum of octaves of noise for FBm
    Float sum = 0, lambda = 1, o = 1;
    for (int i = 0; i < nInt; ++i) {
        sum += o * Noise(lambda * p);
        lambda *= 1.99f; // 读者注：防止在整数点上的噪声值一直是零
        o *= omega;
    }
		// 读者注：加了一点点最后一级的内容，以便超过纳什频率的内容消失得比较自然
		//        不过很奇怪这里加了之后难道不会超过 maxOctaves 吗...
    Float nPartial = n - nInt;
    sum += o * SmoothStep(.3f, .7f, nPartial) * Noise(lambda * p);
    // 读者注：这里好像也没有归一化，不过反正均值还是 0 就不管了？
		return sum;
}

Turbulence

和分型杂色相似的另一种噪声是 Turbulence() 噪声。它在加权的时候使用 Perlin Noise 的绝对值加权，在保证噪声值是正数的同时也引入了导数的不连续性。3 阶和 6 阶的一维 Turbulence() 噪声图像如下：

10.6.3 - 10.6.5 Noise 的应用

这里介绍了三种不同的噪声的应用场景，包括了：

  1. FBm 或 Turbulence 直接作为 Bump Mapping 的材质

  2. 使用两个 FBm 模拟风强和浪高的材质

    这里比较奇怪的是，明明这个材质的 Evaluate 返回的是模板参数的类型，但实际上返回的是两个浮点数的乘积

  3. 使用 FBm 在采样前偏移材质坐标的材质

Martin Z He咕咕咕