PBRT 第三章笔记（基础篇） | Notes for PBRT Chapter 03 - Shapes (basis)

programming | reading notes , , Comments

3.1 Basic Shape Interface

Shape 基类的完整定义如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Shape {
  public:
    // Shape Interface
    Shape(const Transform *ObjectToWorld, const Transform *WorldToObject,
          bool reverseOrientation);
    virtual ~Shape();
    virtual Bounds3f ObjectBound() const = 0;
    virtual Bounds3f WorldBound() const;
    virtual bool Intersect(const Ray &ray, Float *tHit,
                           SurfaceInteraction *isect,
                           bool testAlphaTexture = true) const = 0;
    virtual bool IntersectP(const Ray &ray,
                            bool testAlphaTexture = true) const {
        return Intersect(ray, nullptr, nullptr, testAlphaTexture);
    }
    virtual Float Area() const = 0;
    // Sample a point on the surface of the shape and return the PDF with
    // respect to area on the surface.
    virtual Interaction Sample(const Point2f &u, Float *pdf) const = 0;
    virtual Float Pdf(const Interaction &) const { return 1 / Area(); }

    // Sample a point on the shape given a reference point |ref| and
    // return the PDF with respect to solid angle from |ref|.
    virtual Interaction Sample(const Interaction &ref, const Point2f &u,
                               Float *pdf) const;
    virtual Float Pdf(const Interaction &ref, const Vector3f &wi) const;

    // Returns the solid angle subtended by the shape w.r.t. the reference
    // point p, given in world space. Some shapes compute this value in
    // closed-form, while the default implementation uses Monte Carlo
    // integration; the nSamples parameter determines how many samples are
    // used in this case.
    virtual Float SolidAngle(const Point3f &p, int nSamples = 512) const;

    // Shape Public Data
    const Transform *ObjectToWorld, *WorldToObject;
    const bool reverseOrientation;
    const bool transformSwapsHandedness;
};

所有物体均被定义在物体坐标系下，为了将物体位置在物体坐标系和世界坐标系之间相互转换，此类中储存了两个相反的变换 ObjectToWorld, WorldToObject

布尔值 reverseOrientation 用于判断在处理时是否需要将物体表面的法线方向取反，而 transformSwapsHandedness 则储存了变换 ObjectToWorld 中用于确认手性是否改变的函数 SwapsHandedness() 的返回值，这样就不需要每次进行光线求交时反复调用该函数了。

3.1.1 包围盒

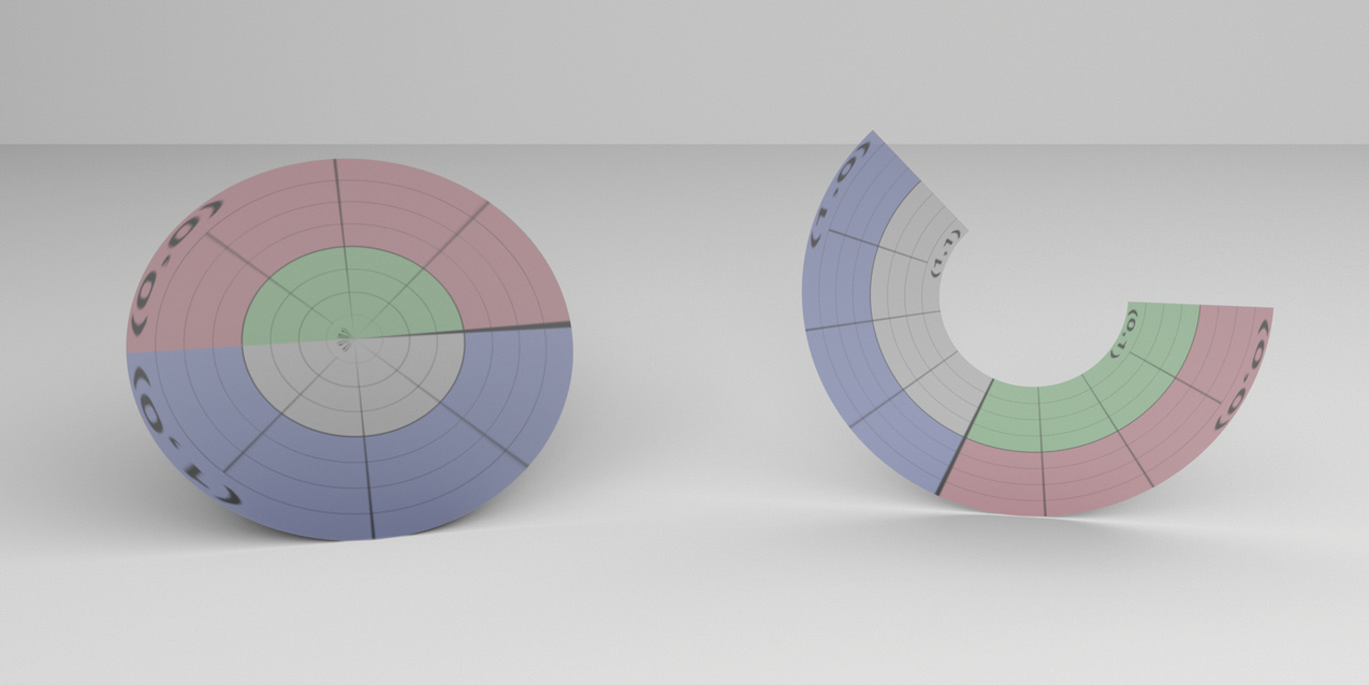
PBRT 使用坐标对齐的边缘包围盒加速渲染的过程。一个物体需要提供它在物体坐标系的包围盒以及在世界坐标系的包围盒的接口。其中在世界坐标系的包围盒接口默认由对物体坐标系的包围盒做变换得到。然而，这是一种极其不高效的做法（如下图所示）

3.1.2 光线 - 包围盒相交

包围盒类提供了光线相交的函数 Bounds3::IntersectP(const Ray&, Float*, Float*) 以得到光线和它自身相交发生的两个时间。它使用了一种快速且有效的方法：

  1. 将光线投影到对每个坐标轴，分别计算光线与各个位置相交的时间范围
  2. 对所有时间范围取交集，检查是否非空

由于需要计算光线各个方向的倒数并通过各个分量的正负检查是否需要交换 tnear / tfar ，PBRT 也提供了一个输入预计算参数版本的函数。

3.1.3 相交测试

Shape 类的派生类需要实现两种相交测试的函数：返回交点位置和表面信息的 Intersect() 和仅返回是否相交的 IntersectP() 由于部分模型提供了 Alpha 裁剪用的材质，这两者均需要传入一个表示是否启用这一功能的参数 testAlphaTexture 。

虽然 PBRT 提供了一种简单地通过调用 Intersect 并忽略其它结果的 IntersectP 的实现，但大部分派生类都会提供更加高效的方法。

3.1.4 表面积

当一个形状被用于面光源时，需要计算其表面积。Shape 基类提供了这一接口。

1
virtual Float Area() const = 0;

3.1.5 单面 / 双面材质（Sidedness）

在大部分渲染系统中均支持 one-sided 的性质，物体在一侧观看时可见，而从另一侧观看时不可见。虽然这一性质在某些情况下提高部分隐藏面删除算法的效率，但在光线追踪的渲染器中并不会有多大的性能影响。这是因为光线追踪的流程中光线相交判断先于法线方向判断，而且这种做法可能导致物理上的不正确。 PBRT 并不支持这一特性。

3.2 Spheres

球体是二次曲面（用二次多项式表示曲面）的一种特殊情况。这类曲面比较容易实现光线相交的算法。数学上，球面被定义为 x2+y2+z2=r2x^2 + y^2 + z^2 = r^2 ，使用极坐标表示为：

{x=rsin⁡θcos⁡ϕy=rsin⁡θsin⁡ϕz=rcos⁡θ\begin{cases} x = r\sin\theta\cos\phi\\ y = r\sin\theta\sin\phi\\ z = r\cos\theta \end{cases}

其中，可以使用 ϕ,θ\phi, \theta 构建一个到 uv∈[0,1]2uv \in [0, 1]^2 的映射，结果如下：

Sphere 类的定义如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Sphere : public Shape {
  public:
    // Sphere Public Methods
    Sphere(const Transform *ObjectToWorld, const Transform *WorldToObject,
           bool reverseOrientation, Float radius, Float zMin, Float zMax,
           Float phiMax)
        : Shape(ObjectToWorld, WorldToObject, reverseOrientation),
          radius(radius),
          zMin(Clamp(std::min(zMin, zMax), -radius, radius)),
          zMax(Clamp(std::max(zMin, zMax), -radius, radius)),
          thetaMin(std::acos(Clamp(std::min(zMin, zMax) / radius, -1, 1))),
          thetaMax(std::acos(Clamp(std::max(zMin, zMax) / radius, -1, 1))),
          phiMax(Radians(Clamp(phiMax, 0, 360))) {}
    Bounds3f ObjectBound() const;
    bool Intersect(const Ray &ray, Float *tHit, SurfaceInteraction *isect,
                   bool testAlphaTexture) const;
    bool IntersectP(const Ray &ray, bool testAlphaTexture) const;
    Float Area() const;
    Interaction Sample(const Point2f &u, Float *pdf) const;
    Interaction Sample(const Interaction &ref, const Point2f &u,
                       Float *pdf) const;
    Float Pdf(const Interaction &ref, const Vector3f &wi) const;
    Float SolidAngle(const Point3f &p, int nSamples) const;

  private:
    // Sphere Private Data
    const Float radius;
    const Float zMin, zMax;
    const Float thetaMin, thetaMax, phiMax;
};

其中的 zMin, zMax, thetaMin, thetaMax 提供了上下的裁剪，phiMax 提供了切面的裁剪

3.2.1 物体坐标下的包围盒

这部分的实现较为直观，这里直接放代码：

1
2
3
4
Bounds3f Sphere::ObjectBound() const {
    return Bounds3f(Point3f(-radius, -radius, zMin),
                    Point3f( radius,  radius, zMax));
}

这种方法并非最优解，比如当 ϕmax⁡\phi_{\max} 的值小于 3π/23\pi / 2 时或当 zMin, zMax 裁切到同一半球上时都可以提供更紧的包围盒。

3.2.2 相交判定

求交的流程如下：

  1. 将光线转换到物体坐标系下，得到方程 (ox+tdx)2+(oy+tdy)2+(oz+tdz)2=r2(o_x + td_x)^2 + (o_y + td_y)^2 + (o_z + td_z)^2 = r^2
  2. 整理为标准二次函数 at2+bt+c=0at^2 + bt + c = 0 并使用公式求解 tt
  3. 获取最近的交点并验证是否超过光线的 tMax
  4. 从 tt 得到交点位置，求解 ϕ,θ\phi, \theta 得到 uv
  5. 使用 thetaMin, thetaMax, phiMax 验证裁剪
  6. 计算误差范围（PBRT 误差管理使用）
  7. 设置 insec 和 tHit 结果

3.2.3 法线的偏导

这部分描述了法线关于 uv 的偏导计算方法，容我以后再看

3.2.4 SurfaceInteraction 初始化

由于在光线的方向向量并不需要单位化，因此在变换后使用这个方向向量计算出的 tt 并不会因为应用了变换而改变。可以直接传入之前用二次方差求根公式计算出来的 tt 设置 tHit 。

Sphere::IntersectP 函数则与需要返回详细信息的 Sphere::Intersect 相似，唯一的区别在于其不需要设置返回信息。

3.2.5 表面积

剪切后的表面积如下（计算过程略）：

1
2
3
Float Sphere::Area() const {
    return phiMax * radius * (zMax - zMin);
}

3.3 Cylinders

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Cylinder : public Shape {
  public:
    // Cylinder Public Methods
    Cylinder(const Transform *ObjectToWorld, const Transform *WorldToObject,
             bool reverseOrientation, Float radius, Float zMin, Float zMax,
             Float phiMax)
        : Shape(ObjectToWorld, WorldToObject, reverseOrientation),
          radius(radius),
          zMin(std::min(zMin, zMax)),
          zMax(std::max(zMin, zMax)),
          phiMax(Radians(Clamp(phiMax, 0, 360))) {}
    Bounds3f ObjectBound() const;
    bool Intersect(const Ray &ray, Float *tHit, SurfaceInteraction *isect,
                   bool testAlphaTexture) const;
    bool IntersectP(const Ray &ray, bool testAlphaTexture) const;
    Float Area() const;
    Interaction Sample(const Point2f &u, Float *pdf) const;

  protected:
    // Cylinder Private Data
    const Float radius, zMin, zMax, phiMax;
};

需要注意的是，这里的柱面并不包含上下底面。

柱面的方程是 x2+y2=r2,z∈(zmin⁡,zmax⁡)x^2+y^2=r^2, z\in(z_{\min},z_{\max}) ，其与球面的处理流程是一致的

3.4 Disks

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Disk : public Shape {
  public:
    // Disk Public Methods
    Disk(const Transform *ObjectToWorld, const Transform *WorldToObject,
         bool reverseOrientation, Float height, Float radius, Float innerRadius,
         Float phiMax)
        : Shape(ObjectToWorld, WorldToObject, reverseOrientation),
          height(height),
          radius(radius),
          innerRadius(innerRadius),
          phiMax(Radians(Clamp(phiMax, 0, 360))) {}
    Bounds3f ObjectBound() const;
    bool Intersect(const Ray &ray, Float *tHit, SurfaceInteraction *isect,
                   bool testAlphaTexture) const;
    bool IntersectP(const Ray &ray, bool testAlphaTexture) const;
    Float Area() const;
    Interaction Sample(const Point2f &u, Float *pdf) const;

  private:
    // Disk Private Data
    const Float height, radius, innerRadius, phiMax;
};

这里的盘面也可以是一个同心圆环，其 uv 就定义在展开的圆环上

光线与盘面相交的算法非常简单，并不需要求解二次方程：由于圆盘的 z 位置是确定的，只需要求光线与该平面的交点，再计算交点是否在盘内即可。特别的，如果该光线与盘面平行（无论在平面内还是在平面外），则视为没有相交。

3.5 Other Quadrics

PBRT 支持的其它二次曲面的计算方法和球面、柱面是一致的

3.5.1 锥面

锥面的函数定义为：

(hxr)2+(hyr)2−(z−h)2=0\left(\frac{h x}{r}\right)^{2}+\left(\frac{h y}{r}\right)^{2}-(z-h)^{2}=0

由其表面 uv 定义的参数方程为：

ϕ=uϕmax⁡x=r(1−v)cos⁡ϕy=r(1−v)sin⁡ϕz=vh\begin{aligned} &\phi=u \phi_{\max } \\ &x=r(1-v) \cos \phi \\ &y=r(1-v) \sin \phi \\ &z=v h \end{aligned}

3.5.2 抛物面

抛物面的函数定义为：

hx2r2+hy2r2−z=0\frac{h x^2}{r^2}+\frac{h y^2}{r^2}-z=0

由其表面 uv 定义的参数方程为：

ϕ=uϕmax⁡z=v(zmax⁡−zmin⁡)r=rmax⁡zzmax⁡x=rcos⁡ϕy=rsin⁡ϕ\begin{aligned} &\phi=u \phi_{\max } \\ &z=v(z_{\max}-z_{\min})\\ &r=r_{\max}\sqrt{z \over z_{\max}}\\ &x=r \cos \phi \\ &y=r \sin \phi \\ \end{aligned}

3.5.2 双曲面

双曲面的函数定义为：

a(x2+y2)−bz2=−1a(x^2+y^2)-bz^2=-1

其中的参数 a,ba,b 是通过传入曲面上的两个关键点决定的。由其表面 uv 定义的参数方程为：

ϕ=uϕmax⁡xr=(1−v)x1+vx2yr=(1−v)y1+vy2x=xrcos⁡ϕ−yrsin⁡ϕy=xrsin⁡ϕ+yrcos⁡ϕz=(1−v)z1+vz2\begin{aligned} \phi &=u \phi_{\max } \\ x_{r} &=(1-v) x_{1}+v x_{2} \\ y_{r} &=(1-v) y_{1}+v y_{2} \\ x &=x_{r} \cos \phi-y_{r} \sin \phi \\ y &=x_{r} \sin \phi+y_{r} \cos \phi \\ z &=(1-v) z_{1}+v z_{2} \end{aligned}

3.6 Triangle Meshes

三角形是 CG 领域中最常用的物体表示方法之一。

为了节省用于储存三角形的内存大小，PBRT 使用顶点列表 + 顶点编号的形式储存三角形物体，而非顺序地储存所有三角形的三个顶点。TriangleMesh 类（结构体）储存了一个三角形网格物体所具有的信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
struct TriangleMesh {
    // TriangleMesh Public Methods
    TriangleMesh(const Transform &ObjectToWorld, int nTriangles,
                 const int *vertexIndices, int nVertices, const Point3f *P,
                 const Vector3f *S, const Normal3f *N, const Point2f *uv,
                 const std::shared_ptr<Texture<Float>> &alphaMask,
                 const std::shared_ptr<Texture<Float>> &shadowAlphaMask,
                 const int *faceIndices);

    // TriangleMesh Data
    const int nTriangles, nVertices;
    std::vector<int> vertexIndices;
    std::unique_ptr<Point3f[]> p;
    std::unique_ptr<Normal3f[]> n;
    std::unique_ptr<Vector3f[]> s;
    std::unique_ptr<Point2f[]> uv;
    std::shared_ptr<Texture<Float>> alphaMask, shadowAlphaMask;
    std::vector<int> faceIndices;
};

需要注意的是 TriangleMesh 对象中储存的三角形位置是在世界坐标系下的位置，因为使用世界坐标的场景多于模型坐标，这样避免了重复进行 ObjectToWorld 坐标转换。

3.6.1 Triangle

PBRT 中，实际上实现了 Shape 接口的三角形物体类型是 Triangle ：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Triangle : public Shape {
  public:
    // Triangle Public Methods
    Triangle(const Transform *ObjectToWorld, const Transform *WorldToObject,
             bool reverseOrientation, const std::shared_ptr<TriangleMesh> &mesh,
             int triNumber);
    Bounds3f ObjectBound() const;
    Bounds3f WorldBound() const;
    bool Intersect(const Ray &ray, Float *tHit, SurfaceInteraction *isect,
                   bool testAlphaTexture = true) const;
    bool IntersectP(const Ray &ray, bool testAlphaTexture = true) const;
    Float Area() const;

    using Shape::Sample;  // Bring in the other Sample() overload.
    Interaction Sample(const Point2f &u, Float *pdf) const;

    // Returns the solid angle subtended by the triangle w.r.t. the given
    // reference point p.
    Float SolidAngle(const Point3f &p, int nSamples = 0) const;

  private:
    // Triangle Private Methods
    void GetUVs(Point2f uv[3]) const;

    // Triangle Private Data
    std::shared_ptr<TriangleMesh> mesh;
    const int *v;
    int faceIndex;
};

每个 Triangle 类表示一个三角形，成员指针 v 指向了这个三角形对应的三个顶点的数组的起始元素。

模型坐标的包围盒与世界坐标的包围盒均可通过简单地合并三个由顶点初始化而成的包围盒得到。

3.6.2 光线-三角形求交

PBRT 的三角形求交算法分为以下几步：

  1. 找到一个仿射变换使得光线在变换后从原点开始沿 +z+z 方向传播
    1. 经过平移变换到原点
    2. 重新排列三个坐标的位置，使得绝对值最大的方向落在 zz 轴上（这是为了避免直接变换可能产生的除零错误）
    3. 计算一个剪切变换让方向对准 zz 轴
  2. 将这个变换同样应用于三角形的顶点上
  3. 在 xOyxOy 平面上测试点 (0,0)(0, 0) 是否在三角形内
    1. 考虑叉乘的特性，给定两点 p0,p1p_0, p_1 确定一条有向的直线，对于任意的第三点 pp ，通过构造向量 p0p1→,p0p→\overrightarrow{p_0 p_1}, \overrightarrow{p_0 p} 并计算他们的叉乘，可以判断 p 点在直线的左侧、右侧还是直线上。
    2. 判断一个点是否在三角形内，只要顺时针遍历三角形的三条边并判断该点是否都在三条边的同一侧即可（特别地，当三个叉乘值均为零则说明三角形与 zz 轴平行，算作不相交）
  4. 考虑叉乘的几何特性，上一步骤中得到的叉乘结果同样可以看作内部的小三角形的面积的一半。用这一特点可以计算三角形的重心坐标 bi=ei/∑kekb_i = e_i / \sum^k e_k ，重心坐标可以用于给法线、uv 等顶点特性插值，满足 b0+b1+b2=1, b0p0+b1p1+b2p2=pb_0 + b_1 + b_2 = 1,\ b_0p_0 + b_1p_1 + b_2p_2 = p
  5. 使用上述的重心坐标计算出三角形与 zz 轴相交的位置，并将其与光线的 tMax 比较以判定是否超出光线范围或者在光线方向的另一侧。为了匹配三角形顶点选择顺序带来的符号变化，实际的比较方法如下：

∑ieizi<tmax⁡∑ieiif∑iei>0∑ieizi>tmax⁡∑ieiotherwise\begin{aligned} & \sum_ie_iz_i < t_{\max}\sum_ie_i & if \sum_ie_i > 0\\ & \sum_ie_iz_i > t_{\max}\sum_ie_i & otherwise \end{aligned}

对于位置关于 uv 的偏导，我们使用一次展开表示面上的某一点：

pi=po+ui∂p∂u+vi∂p∂vp_i = p_o + u_i\frac{\partial p}{\partial u} + v_i\frac{\partial p}{\partial v}

对于交点 po=pp_o = p 而言，假设三角形的三个顶点均满足上述关系，则有：

(u0−u2v0−v2u1−u2v1−v2)(∂p/∂u∂p/∂v)=(p0−p2p1−p2)(∂p/∂u∂p/∂v)=(u0−u2v0−v2u1−u2v1−v2)−1(p0−p2p1−p2)\begin{aligned}&\left(\begin{array}{ll}u_{0}-u_{2} & v_{0}-v_{2} \\u_{1}-u_{2} & v_{1}-v_{2}\end{array}\right)\left(\begin{array}{l}\partial \mathrm{p} / \partial u \\\partial \mathrm{p} / \partial v\end{array}\right)=\left(\begin{array}{l}\mathrm{p}_{0}-\mathrm{p}_{2} \\\mathrm{p}_{1}-\mathrm{p}_{2}\end{array}\right) \\&\left(\begin{array}{l}\partial \mathrm{p} / \partial u \\\partial \mathrm{p} / \partial v\end{array}\right)=\left(\begin{array}{ll}u_{0}-u_{2} & v_{0}-v_{2} \\u_{1}-u_{2} & v_{1}-v_{2}\end{array}\right)^{-1}\left(\begin{array}{l}\mathrm{p}_{0}-\mathrm{p}_{2} \\\mathrm{p}_{1}-\mathrm{p}_{2}\end{array}\right)\end{aligned}

最后，在设置返回信息和报告相交情况前，需要根据传入的 testAlphaTexture 开关和模型是否具有 alphaMask 的情况验证是否将该三角形剔除。

虽然 SurfaceInteraction 的构造函数会初始化法线，但在本类中会以如下方式使用自己的方法生成法线：

  • 如果有插值得到的法线，优先使用它
  • 否则使用之前计算的三角形的两条边的正则化叉积

3.6.3 Shading Geometry

Triangle 类会尝试使用插值初始化用于着色的几何体，完整过程如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// Compute shading normal _ns_ for triangle
Normal3f ns;
if (mesh->n) {
    ns = (b0 * mesh->n[v[0]] + b1 * mesh->n[v[1]] + b2 * mesh->n[v[2]]);
    if (ns.LengthSquared() > 0)
        ns = Normalize(ns);
    else
        ns = isect->n;
} else
    ns = isect->n;

// Compute shading tangent _ss_ for triangle
Vector3f ss;
if (mesh->s) {
    ss = (b0 * mesh->s[v[0]] + b1 * mesh->s[v[1]] + b2 * mesh->s[v[2]]);
    if (ss.LengthSquared() > 0)
        ss = Normalize(ss);
    else
        ss = Normalize(isect->dpdu);
} else
    ss = Normalize(isect->dpdu);

// Compute shading bitangent _ts_ for triangle and adjust _ss_
Vector3f ts = Cross(ss, ns);
if (ts.LengthSquared() > 0.f) {
    ts = Normalize(ts);
    ss = Cross(ts, ns);
} else
    CoordinateSystem((Vector3f)ns, &ss, &ts);

// Compute $\dndu$ and $\dndv$ for triangle shading geometry
Normal3f dndu, dndv;
if (mesh->n) {
    // Compute deltas for triangle partial derivatives of normal
    Vector2f duv02 = uv[0] - uv[2];
    Vector2f duv12 = uv[1] - uv[2];
    Normal3f dn1 = mesh->n[v[0]] - mesh->n[v[2]];
    Normal3f dn2 = mesh->n[v[1]] - mesh->n[v[2]];
    Float determinant = duv02[0] * duv12[1] - duv02[1] * duv12[0];
    bool degenerateUV = std::abs(determinant) < 1e-8;
    if (degenerateUV) {
        Vector3f dn = Cross(Vector3f(mesh->n[v[2]] - mesh->n[v[0]]),
                            Vector3f(mesh->n[v[1]] - mesh->n[v[0]]));
        if (dn.LengthSquared() == 0)
            dndu = dndv = Normal3f(0, 0, 0);
        else {
            Vector3f dnu, dnv;
            CoordinateSystem(dn, &dnu, &dnv);
            dndu = Normal3f(dnu);
            dndv = Normal3f(dnv);
        }
    } else {
        Float invDet = 1 / determinant;
        dndu = (duv12[1] * dn1 - duv02[1] * dn2) * invDet;
        dndv = (-duv12[0] * dn1 + duv02[0] * dn2) * invDet;
    }
} else
    dndu = dndv = Normal3f(0, 0, 0);
if (reverseOrientation) ts = -ts;
isect->SetShadingGeometry(ss, ts, dndu, dndv, true);

3.6.4 表面积

使用叉乘模长的一半求面积

3.7 Curves ⚠️

这部分描述了曲线类型的形状，容我以后再看。

3.8 Subdivision Surfaces ⚠️

这部分描述了细分表面类型的形状，容我以后再看。

3.9 Managing Rounding Error ⚠️

这部分描述了 PBRT 是解决浮点错误的方法，容我以后再看。

Martin Z He咕咕咕